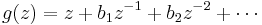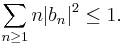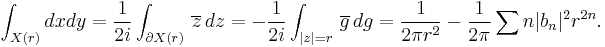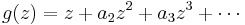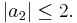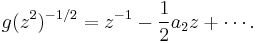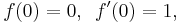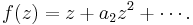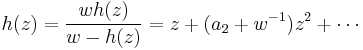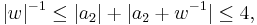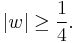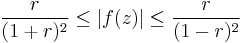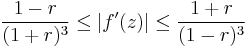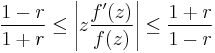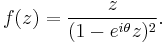Koebe quarter theorem
In complex analysis, a branch of mathematics, the Koebe 1/4 theorem states that the image of an injective analytic function 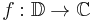 from the unit disk
from the unit disk 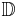 onto a subset of the complex plane contains the disk whose center is
onto a subset of the complex plane contains the disk whose center is 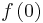 and whose radius is
and whose radius is 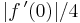 . The theorem is named after Paul Koebe, who conjectured the result in 1907. The theorem was proven by Ludwig Bieberbach in 1914. The Koebe function ƒ(z) = z/(1 − z)2 shows that the constant 1/4 in the theorem cannot be improved.
. The theorem is named after Paul Koebe, who conjectured the result in 1907. The theorem was proven by Ludwig Bieberbach in 1914. The Koebe function ƒ(z) = z/(1 − z)2 shows that the constant 1/4 in the theorem cannot be improved.
A related result is the Schwarz lemma, and a notion related to both is conformal radius.
Contents |
Gronwall's area theorem
Suppose that
is univalent in 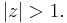 Then
Then
In fact, if r > 1, the complement of the image of the disk |z| > r is a bounded domain X(r). Its area is given by
Since the area is positive, the result follows by letting r decrease to 1. The above proof shows quality holds if and only if the complement of the image of g has zero area, i.e. Lebesgue measure zero.
This result was proved in 1914 by the Swedish mathematician Thomas Hakon Gronwall.
Bieberbach's coefficient inequality for univalent functions
Let
be univalent in 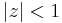 . Then
. Then
This follows by applying Gronwall's area theorem to the odd univalent function
Equality holds if and only if g is a rotation of the Koebe function.
This result was proved by Ludwig Bieberbach in 1916 and provided the basis for his celebrated conjecture that |an| ≤ n, proved in 1985 by Louis de Branges.
Proof of quarter theorem
Applying an affine map, it can be assumed that
so that
If w is not in 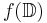 , then
, then
is univalent in 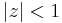 .
.
Applying the coefficient inequality to f and h gives
so that
Koebe distortion theorem
The Koebe distortion theorem gives a series of bounds for a univalent function and its derivative. It is a direct consequence of Bieberbach's inequality for the second coefficient and the Koebe quarter theorem.[1]
Let f(z) be a univalent function on |z| < 1 normalized so that f(0) = 0 and f'(0) = 0 and let r = |z|. Then
with equality if and only if f is a Koebe function
Notes
- ^ Pommerenke 1975, p. 21-22
References
- Bieberbach, Ludwig (1916), Über die Koeffizienten derjenigen Polenzreihen, welche eine schlichte Abbildung des Einheitskreises vermitteln, pp. 940-955
- Carleson, L.; Gamelin, T. D. W. (1993), Complex dynamics, Universitext: Tracts in Mathematics, Springer-Verlag, pp. 1-2, ISBN 0-387-97942-5
- Duren, P. L. (1983), Univalent functions, Grundlehren der Mathematischen Wissenschaften, 259, Springer-Verlag, ISBN 0-387-90795-5
- Gronwall, T.H. (1914), "Some remarks on conformal representation", Ann. of Math. 16: 72-76
- Nehari, Zeev (1952), Conformal mapping, Dover, pp. 248-249, ISBN 0-486-61137-X
- Pommerenke, C. (1975), Univalent functions, with a chapter on quadratic differentials by Gerd Jensen, Studia Mathematica/Mathematische Lehrbücher, 15, Vandenhoeck & Ruprecht
- Rudin, Walter (1987). Real and Complex Analysis. Series in Higher Mathematics (3 ed.). McGraw-Hill. ISBN 0070542341. MR924157.
- Koebe 1/4 theorem at PlanetMath